চিওসের হিপোক্রাক্রেটস (ফ্ল। সি। 460 বিসি) প্রমাণ করেছে যে চক্রাকার আকারের বৃত্তাকার আরাকের মধ্যে অবস্থিত অঞ্চলগুলি, যা লুনস নামে পরিচিত, একেবারে একটি পুনর্গঠনযোগ্য অঞ্চল বা চতুর্ভুজ হিসাবে প্রকাশ করা যেতে পারে। নিম্নলিখিত সাধারণ ক্ষেত্রে, ডান ত্রিভুজের পাশের চারদিকে বিকশিত দুটি লুনের ত্রিভুজটির সমান একটি মিলিত অঞ্চল রয়েছে।
-
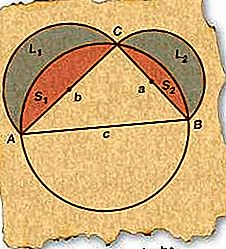
ডান ΔABC দিয়ে শুরু করে, এমন একটি বৃত্ত আঁকুন যার ব্যাসটি AB (পাশের সি), হাইপোপেনসিসের সাথে মিলে যায়। যেহেতু কোনও অনুভূতির জন্য বৃত্তের ব্যাসের সাথে আঁকা কোনও ডান ত্রিভুজ অবশ্যই বৃত্তের মধ্যে খোদাই করা উচিত, সি অবশ্যই বৃত্তের মধ্যে থাকা উচিত।
-
চিত্রের মতো ডায়ামিটার এসি (পাশের বি) এবং বিসি (পাশের ক) দিয়ে অর্ধবৃত্তগুলি আঁকুন।
-
চিত্রটিতে উল্লিখিত ফলাফলগুলি L 1 এবং L 2 এবং ফলাফলগুলি S 1 এবং S 2 লেবেল করুন ।
-
এখন লুনগুলির যোগফল (এল 1 এবং এল 2) অবশ্যই অর্ধবৃত্তগুলির সমষ্টি (এল 1 + এস 1 এবং এল 2 + এস 2) এর সাথে দুটি বিভাগকে বিয়োগ করে (এস 1 এবং এস 2) বিয়োগ করবে । সুতরাং, এল 1 + এল 2 = π / 2 (বি / 2) 2 - এস 1 + π / 2 (ক / 2) 2 - এস 2 (যেহেতু একটি বৃত্তের ক্ষেত্রফলের ব্যাসার্ধের দ্বিগুণ)।
-
বিভাগগুলির যোগফল (এস 1 এবং এস 2) ত্রিভুজের ক্ষেত্রের বিয়োগ বিয়োগের উপর ভিত্তি করে অর্ধবৃত্তের ক্ষেত্রফলের সমান। সুতরাং, এস 1 + এস 2 = π / 2 (সি / 2) 2 - Δএবসি।
-
5 ধাপে 4 পদক্ষেপে অভিব্যক্তিটি প্রতিস্থাপন এবং সাধারণ পদগুলি নির্ধারণ করে, L 1 + L 2 = π / 8 (a 2 + b 2 - c 2) + CABC।
-
পাইথাগোরিয়ান উপপাদ্য দ্বারা ∠এসিবি = 90 °, একটি 2 + বি 2 - সি 2 = 0 থেকে। সুতরাং, এল 1 + এল 2 = ΔABC।
হিপোক্রেটিস বিভিন্ন ধরণের লুনকে বর্গক্ষেত্র করতে পেরেছিল, কিছুটি অর্কেচক্রের চেয়ে বৃহত্তর এবং তার চেয়ে কম আরকগুলির উপর ছিল এবং তিনি অন্তর্নিহিত করেছিলেন, যদিও তিনি বিশ্বাস করেননি, তার পদ্ধতিটি পুরো বৃত্তটিকে বর্গাকার করতে পারে। শাস্ত্রীয় যুগের শেষে, বোথিয়াস (সি। বিজ্ঞাপন 470–524), যার ইউক্লিডের স্নিপেটের ল্যাটিন অনুবাদগুলি অর্ধ সহস্রাব্দের জন্য জ্যামিতির ঝলকানি রাখবে, উল্লেখ করেছে যে কেউ বৃত্তের স্কোয়ারিং সম্পন্ন করেছে। অজানা প্রতিভা লুন বা অন্য কোনও পদ্ধতি ব্যবহার করেছিল কিনা তা জানা যায়নি, কারণ জায়গার অভাবে বোথিয়াস বিক্ষোভ দেখায়নি। তিনি এইভাবে বৃত্তের চতুর্ভুজটির চ্যালেঞ্জকে একত্রিত করে জ্যামিতির টুকরো টুকরো টুকরো করে তা সম্পাদন করার ক্ষেত্রে দৃশ্যত কার্যকর করেছিলেন। ইউরোপীয়রা এই অনর্থক কাজটিকে আলোকিতকরণের জন্য ভালভাবে রেখেছিল। পরিশেষে, ১75 in৫ সালে প্যারিস একাডেমি অফ সায়েন্সেস এর কাছে জমা দেওয়া অনেকগুলি সমাধানে ভুলগুলি চিহ্নিত করার কাজ থেকে বিরক্ত হয়ে বৃত্তাকার স্কোয়ারদের সাথে আরও কিছু করতে অস্বীকার করেছিল।